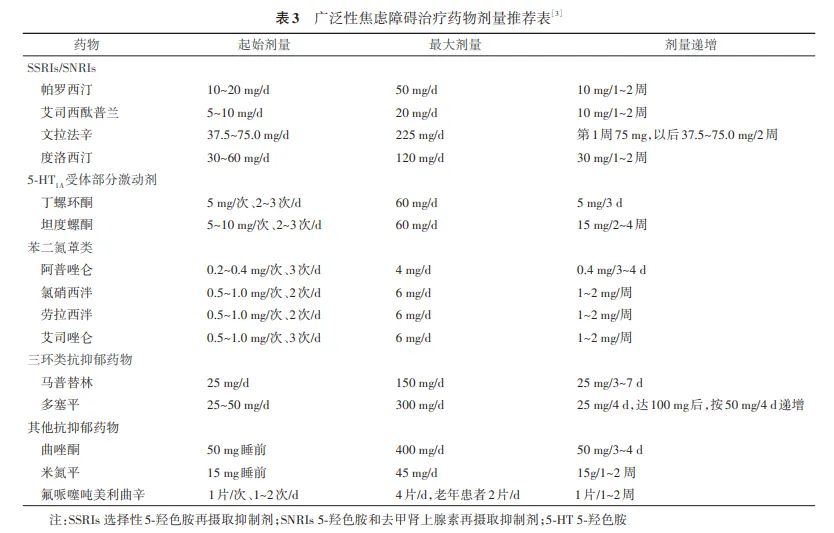
这种建模方式既简单又高效,利用Simulink工具和雅克比矩阵,可以将复杂的非线性模型转化为易于控制的线性模型。此外,它还能构建出二次型最优控制器,对车辆运动学模型进行闭环仿真。不妨看看!

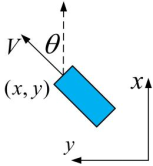
运动学模型难题
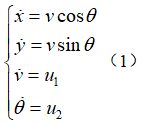
车辆在行驶过程中,其模型揭示了横竖方向间存在非线性互动的特征。这一特点让控制系统设计变得异常繁难,很多人在初期设计阶段都感到困惑。尽管众多专业人士投入了众多时间和精力去应对这种非线性问题,但实际效果往往不尽如人意。因此,寻求有效的解决之道显得尤为重要。
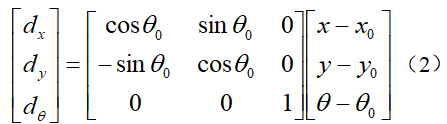
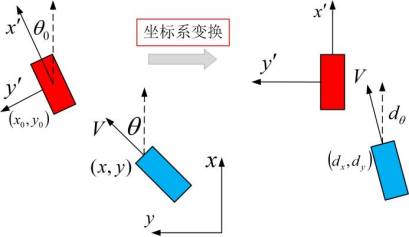
横纵向系统解耦
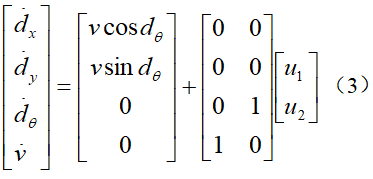


为了简化设计流程,我们可以将水平与垂直的系统分开来处理。在具体应用中,这样操作有助于把复杂问题分解成几个较为简单的部分。分解完成后,我们可以根据横纵子系统的特性,分别设计出更合适的控制器,从而为后续的仿真与控制工作奠定坚实的基石。
纵向控制系统策略
纵向控制系统设计简明,仅由一个输入和一个输出构成,非常适合运用PID控制方法。在具体操作上,PID控制可依据车辆实际行驶速度与设定速度之间的差异,精确调整控制命令,确保车辆速度能快速且平稳地达到设定目标。以自动巡航系统为例,这种控制方式已被普遍采用。
横向控制系统主要职能是确保车辆沿着预定路线平稳行驶。通过解耦处理后的横向动力学模型,我们可以清晰掌握车辆的横向运动以及相关的系统矩阵。运用线性二次型调节器(LQR)技术,通过选择恰当的二次型性能指标,对黎卡提方程进行持续计算,最终计算出最优的状态反馈控制增益矩阵。
求解算法与工具

MATLAB软件能够解决黎卡提方程和最优控制问题。在解决线性时变系统或线性变参(LPV)模型的控制器实时计算时,通常会使用迭代法。控制系统工具箱里的care函数和lqr函数也可用于计算,但在某些特定情况下,迭代法的效果更佳。
闭环仿真与分析
构建一个完整的闭环模拟体系,其中包含了解耦的横纵控制器。在垂直方向上,我们运用PID控制方法;而在水平方向上,则选择了LQR控制策略。经过线性化处理后的模型,既可以通过计算雅克比矩阵获得,也可以通过Simulink仿真模型来构建。车辆一旦设定好起点、行驶路径和速度,便可通过MATLAB中的lqr函数,轻松解决二次型最优控制问题,从而实现闭环仿真与数据分析。
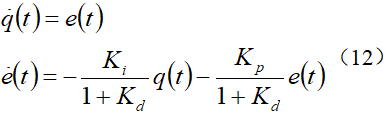

在车辆仿真运动中,您可能遇到了一些难题。不妨点个赞,转发这篇文章,然后在评论区留下您的见解,咱们一起来探讨和交流。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请联系本站,一经查实,本站将立刻删除。如若转载,请注明出处:http://www.mayuv.com/html/tiyuwenda/9809.html